เคยสงสัยไหมว่า Y=f(x) หมายถึงอะไรในการบริหารโครงการ? แนวคิดอันทรงพลังนี้ไม่ได้มีไว้สำหรับนักคณิตศาสตร์เท่านั้น มันเป็นตัวเปลี่ยนเกมสำหรับความสำเร็จของโครงการ ช่วยให้คุณวางแผน ว่าปัจจัยนำเข้าส่งผลต่อผลลัพธ์อย่างไร
Y=f(x) ไม่ใช่แค่สูตรคำนวณเท่านั้น แต่เป็นวิธีในการทำความเข้าใจและควบคุมตัวแปรของโครงการของคุณ เพิ่มประสิทธิภาพ และตัดสินใจได้อย่างชาญฉลาดยิ่งขึ้น
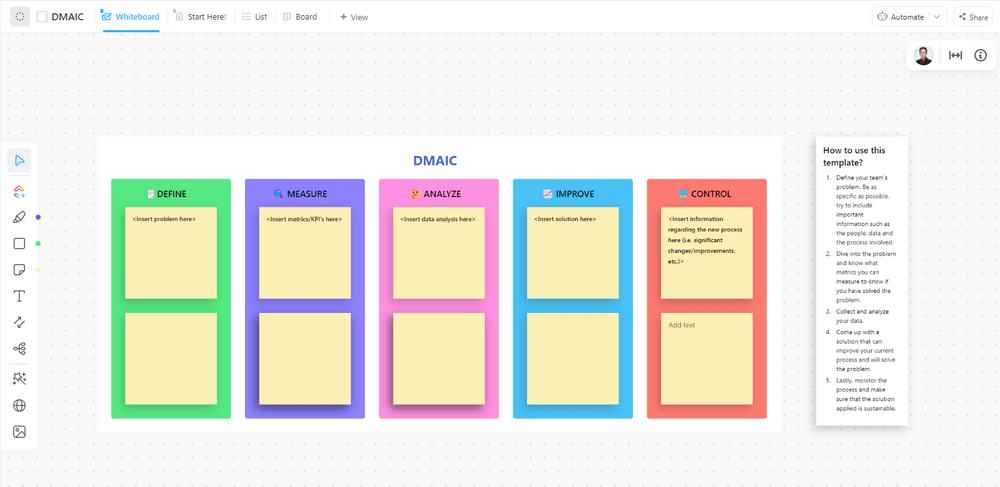
ในบทความนี้ คุณจะได้เรียนรู้วิธีการนำ Y=f(x) ไปใช้ในโครงการของคุณ เราจะอธิบาย กรอบงาน DMAIC และแสดงให้คุณเห็นว่ามันเชื่อมโยงกับแนวคิดนี้อย่างไร นอกจากนี้ คุณยังจะได้เรียนรู้แนวทางปฏิบัติที่ดีที่สุดเพื่อใช้ประโยชน์จาก Y=f(x) ในโครงการของคุณอย่างเต็มที่
ไม่ว่าคุณจะเป็นมือใหม่กับเครื่องมือ Six Sigmaหรือเป็นผู้เชี่ยวชาญที่มีประสบการณ์ ข้อมูลเชิงลึกเหล่านี้จะช่วยให้คุณเป็นผู้จัดการโครงการที่มีประสิทธิภาพมากขึ้น
Y=f(x) ในซิกซ์ซิกมา
Y=f(x) เป็นรากฐานสำคัญของวิธีการซิกซ์ซิกมา ช่วยให้เรา แสดงผลลัพธ์ที่ต้องการในเชิงปริมาณได้
ในการบริหารโครงการ สมการ Y=f(x) เป็นการแทนทางคณิตศาสตร์ของ ความสัมพันธ์เชิงฟังก์ชันระหว่างปัจจัยนำเข้าของโครงการ (x) และผลลัพธ์ของโครงการ (Y) โดยพื้นฐานแล้ว หมายความว่าผลลัพธ์ของโครงการเป็นฟังก์ชันของตัวแปรนำเข้าและปัจจัยที่มีอิทธิพลต่อตัวแปรเหล่านั้น
กล่าวอีกนัยหนึ่ง ผลลัพธ์ที่คุณได้รับ (Y) ขึ้นอยู่กับองค์ประกอบที่คุณใส่เข้าไปในโครงการ (x) และวิธีการที่องค์ประกอบเหล่านั้นถูกผสมผสานกัน (f)
เมื่อเริ่มต้นโครงการ อาจเป็นเรื่องท้าทายในการกำหนดปัญหาเบื้องต้นและระบุผลลัพธ์ที่ต้องการอย่างชัดเจน การใช้สมการ Y=f(x) ตั้งแต่แรกจะช่วยให้คุณต้องทำความเข้าใจ 'Y' อย่างชัดเจน ซึ่งหมายถึงผลลัพธ์ที่คุณต้องการให้เกิดขึ้นจากการดำเนินงาน
แนวทางนี้บังคับให้คุณและทีมโครงการของคุณ มองผลลัพธ์เป็นคำที่สามารถวัดได้ ซึ่งเป็นการสร้างฐานที่มั่นคงสำหรับความสำเร็จของโครงการของคุณ ไม่ว่าคุณจะเลือกใช้วิธีการบริหารโครงการแบบใดก็ตาม
การถอดรหัสสูตร Y=f(x)
เพื่อใช้ประโยชน์จากพลังของ Y=f(x) ในโครงการของคุณ คุณจำเป็นต้องเข้าใจองค์ประกอบหลักของมัน:
- Y (ผลลัพธ์): นี่คือผลลัพธ์หรือผลผลิตที่ได้จากโครงการ ซึ่งอาจเป็นได้ทั้งผลิตภัณฑ์หรือบริการที่ส่งมอบแล้ว ไปจนถึงผลลัพธ์เฉพาะ เช่น ยอดขายที่เพิ่มขึ้น หรือความพึงพอใจของลูกค้าที่ดีขึ้น
- ฟังก์ชัน (Function): หมายถึงกระบวนการหรือขั้นตอนที่เปลี่ยนแปลงข้อมูลนำเข้าให้กลายเป็นผลลัพธ์ตามที่ต้องการ ซึ่งอาจประกอบด้วยชุดของงาน กิจกรรม หรือการตัดสินใจที่ส่งผลต่อเป้าหมายของโครงการ
- x (ข้อมูลนำเข้า): สิ่งเหล่านี้อาจรวมถึงทรัพยากร (เช่น เวลา, เงิน, บุคลากร), เครื่องมือ, เทคนิค, หรือปัจจัยภายนอก (เช่น สภาพตลาด, ความก้าวหน้าทางเทคโนโลยี)
- ε (ข้อผิดพลาด): ตัวนี้แสดงถึงระดับของความไม่แน่นอนหรือความแตกต่างระหว่างผลลัพธ์ที่คาดหวังกับผลลัพธ์ที่เกิดขึ้นจริงเมื่อกระบวนการถูกนำไปใช้

ฟังก์ชันทางคณิตศาสตร์ Y=f(x) อธิบายความสัมพันธ์ระหว่างตัวแปรตาม (Y) กับตัวแปรอิสระหนึ่งตัวหรือมากกว่า (x) โดยแสดงให้เห็นว่าการเปลี่ยนแปลงของตัวแปรอิสระส่งผลให้เกิดการเปลี่ยนแปลงของตัวแปรตามอย่างไร
มาทำความเข้าใจแนวคิดนี้ด้วยตัวอย่างที่นำไปใช้ได้จริง
พิจารณาโครงการพัฒนาซอฟต์แวร์:
Y: แอปพลิเคชันซอฟต์แวร์ที่ทำงานได้อย่างสมบูรณ์ ปราศจากข้อบกพร่อง
f: กระบวนการพัฒนา ซึ่งรวมถึงการรวบรวมความต้องการ การออกแบบ การเขียนโค้ด การทดสอบ และการนำไปใช้งาน
x: ปัจจัยนำเข้า เช่น ทักษะของทีมพัฒนา งบประมาณของโครงการ ภาษาโปรแกรมที่เลือกใช้ และระยะเวลาของโครงการ
ในตัวอย่างนี้ คุณภาพและความสำเร็จของแอปพลิเคชันซอฟต์แวร์ (Y) ขึ้นอยู่กับความมีประสิทธิภาพของกระบวนการพัฒนา (f) และความพร้อมใช้งานและคุณภาพของข้อมูลนำเข้า (x)
ประโยชน์ของ Y=f(x) สำหรับผู้จัดการโครงการ
การนำ Y=f(x) มาใช้ในแนวทางการบริหารโครงการของคุณมีประโยชน์สำคัญหลายประการ:
- ความเข้าใจที่ดีขึ้นเกี่ยวกับสาเหตุและผลลัพธ์: Y=f(x) ช่วยให้คุณเข้าใจความสัมพันธ์ระหว่างปัจจัยนำเข้าและผลลัพธ์ ทำให้คุณสามารถตัดสินใจได้อย่างมีข้อมูลมากขึ้นตลอดโครงการของคุณ
- การวัดผลการดำเนินงานที่เพิ่มประสิทธิภาพ: โดยการกำหนดผลลัพธ์ที่ต้องการ (Y) และปัจจัยที่มีอิทธิพลต่อผลลัพธ์เหล่านั้น (x) อย่างชัดเจน คุณสามารถวัดผลการดำเนินงานของโครงการได้อย่างมีประสิทธิภาพมากขึ้นและระบุพื้นที่ที่ต้องปรับปรุง
- การตัดสินใจโดยใช้ข้อมูลเป็นฐาน: Y=f(x) ช่วยให้คุณสามารถเข้าใจและปรับปรุงความสัมพันธ์ระหว่างปัจจัยนำเข้าและตัวชี้วัดผลลัพธ์ที่ต้องการได้อย่างเป็นระบบ วิธีการที่ขับเคลื่อนด้วยข้อมูลนี้ช่วยลดข้อบกพร่อง ข้อผิดพลาด และความแปรปรวน พร้อมทั้งเพิ่มคุณภาพของผลิตภัณฑ์และความพึงพอใจของลูกค้า
- การพัฒนาอย่างต่อเนื่อง: การใช้ประโยชน์จาก Y=f(x) จะมอบเครื่องมือที่ทรงพลังให้คุณเพื่อขับเคลื่อนการพัฒนาอย่างต่อเนื่อง ลดต้นทุน และบรรลุการเติบโตที่ยั่งยืนในโครงการของคุณ
- นวัตกรรมและความสามารถในการปรับตัว: ความสามารถในการจำลองและทำนายผลกระทบที่การเปลี่ยนแปลงของปัจจัยต่าง ๆ มีต่อผลลัพธ์ จะช่วยให้คุณสามารถสร้างนวัตกรรมและปรับตัวได้ ในสภาพแวดล้อมตลาดที่เปลี่ยนแปลงอย่างรวดเร็ว สิ่งนี้จะมอบความได้เปรียบทางการแข่งขันที่ชัดเจนให้กับคุณ
- การแก้ปัญหาอย่างมีประสิทธิภาพ: Y=f(x) นำทางคุณผ่านแผนที่ DMAIC (กำหนด, วัด, วิเคราะห์, ปรับปรุง, ควบคุม) มอบแนวทางที่มีโครงสร้างสำหรับการแก้ปัญหาในโครงการของคุณ
อ่านเพิ่มเติม:ตัวอย่างการปรับปรุงกระบวนการอย่างต่อเนื่อง
ความท้าทายในการใช้กรอบแนวคิด Y=f(x)
แม้ว่า Y=f(x) จะมีประโยชน์มากมาย แต่ก็มีความท้าทายที่อาจเกิดขึ้นได้เช่นกัน ซึ่งบางประการได้แก่:
- การขาดข้อมูล: ในบางกรณี ผู้จัดการโครงการอาจไม่มีข้อมูลเพียงพอที่จะวัดความสัมพันธ์ระหว่างปัจจัยนำเข้าและผลลัพธ์ได้อย่างแม่นยำ ซึ่งอาจทำให้สมการไม่มีประสิทธิภาพ
- ความซับซ้อนของข้อมูลนำเข้า: โครงการจำนวนมากเกี่ยวข้องกับข้อมูลนำเข้าจำนวนมากที่มีความสัมพันธ์กัน ทำให้ยากต่อการระบุและวัดปัจจัยที่เกี่ยวข้องทั้งหมดได้อย่างถูกต้อง
- ความไม่แน่นอนและความเสี่ยง: โครงการมีความไม่แน่นอนโดยธรรมชาติ และเหตุการณ์ที่ไม่คาดคิดสามารถส่งผลกระทบอย่างมีนัยสำคัญต่อความสัมพันธ์ระหว่างปัจจัยนำเข้าและผลลัพธ์ ซึ่งทำให้ยากที่จะสร้างสมการที่เป็นรูปธรรม
- ปัจจัยเชิงคุณภาพ: ปัจจัยหลายประการที่มีอิทธิพลต่อผลลัพธ์ของโครงการเป็นปัจจัยเชิงคุณภาพ ซึ่งทำให้ยากต่อการวัดและประเมินค่าได้อย่างแม่นยำ สิ่งนี้อาจจำกัดประโยชน์ของสมการ
- การพึ่งพาอาศัยกัน: ปัจจัยนำเข้าหลายอย่างมักมีความพึ่งพาอาศัยกัน และการเปลี่ยนแปลงในปัจจัยนำเข้าหนึ่งอาจส่งผลกระทบต่อปัจจัยนำเข้าอื่น ๆ หลายประการได้ ซึ่งอาจทำให้ยากต่อการแยกผลกระทบของปัจจัยแต่ละตัว
- การต่อต้านจากทีม:การนำการปรับปรุงกระบวนการตามแบบY=f(x) อาจเผชิญกับการต่อต้านจากสมาชิกทีมที่ไม่คุ้นเคยกับวิธีการทางสถิติ ในกรณีเช่นนี้ ผู้จัดการโครงการจะต้องนำกลยุทธ์การจัดการการเปลี่ยนแปลงที่มีประสิทธิภาพมาใช้
🎉ทรัพยากรโบนัส:คู่มือสำหรับรักษาโครงการของคุณให้อยู่ในเส้นทางที่ถูกต้อง!
การนำ Y=f(x) ไปใช้ผ่านกรอบการทำงาน DMAIC
DMAIC (กำหนด, วัด, วิเคราะห์, ปรับปรุง, ควบคุม) เป็นวิธีการแก้ปัญหาที่มีโครงสร้างซึ่งมักใช้ในโครงการ Six Sigma มันให้แนวทางที่เป็นระบบในการระบุและแก้ไขสาเหตุที่แท้จริงของข้อบกพร่องหรือความไม่มีประสิทธิภาพ แนวคิด Y=f(x) สามารถผสานเข้ากับกรอบงาน DMAIC ได้อย่างราบรื่นเพื่อเพิ่มประสิทธิภาพในการแก้ปัญหาและการปรับปรุงกระบวนการ
นี่คือวิธีที่คุณสามารถใช้ DMAIC เพื่อนำ Y=f(x) ไปสู่การปฏิบัติ
ขั้นตอนที่ 1. กำหนด: การตั้งเป้าหมายโครงการ
ก้าวแรกสู่ความสำเร็จของโครงการคือการระบุสิ่งที่คุณต้องการบรรลุ นี่คือจุดที่ขั้นตอนการ กำหนด มีประโยชน์ มันเกี่ยวกับการเข้าใจ 'Y' ในสมการ Y=f(x) ของคุณ—ผลลัพธ์ที่คุณต้องการ
เริ่มต้นด้วยการถามตัวเองว่าโครงการของคุณมี ปัญหาทางธุรกิจหรือกระบวนการที่เฉพาะเจาะจงและชัดเจนที่ต้องการแก้ไข หรือไม่
บางครั้ง คำตอบก็ชัดเจน แต่บ่อยครั้ง คุณอาจต้องค้นหาให้ลึกขึ้น หากมันไม่ชัดเจน ให้ทำงานเพื่อ ได้ภาพที่ชัดเจนของ 'Y' ของคุณ—ปัญหาในกระบวนการที่คุณพยายามแก้ไข—ในแง่ที่สามารถวัดได้ซึ่งสอดคล้องกับเป้าหมายของโครงการของคุณ
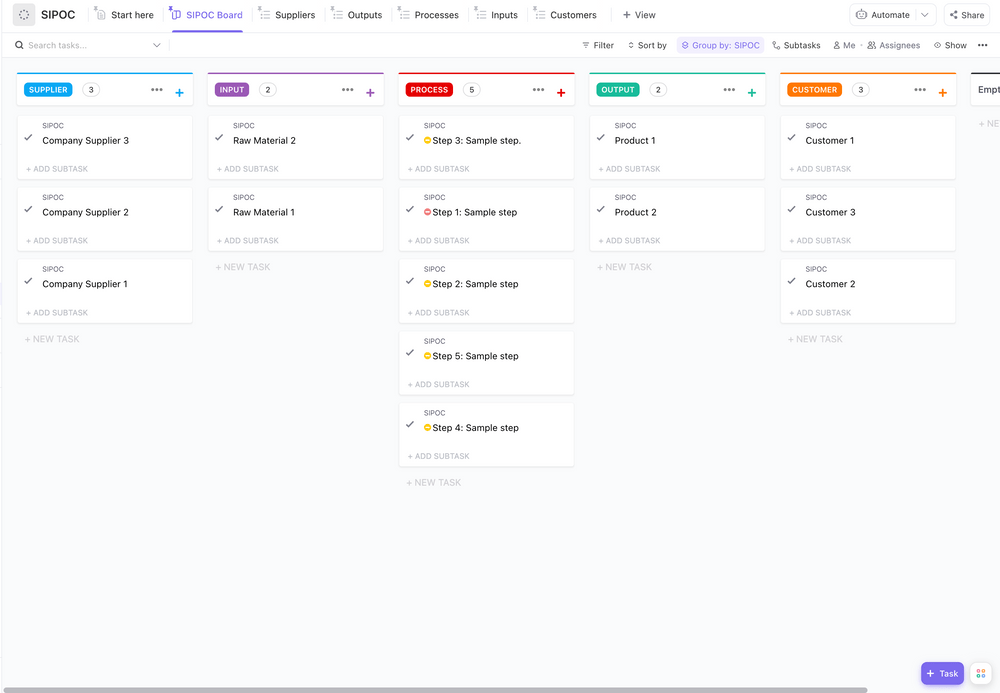
เครื่องมือที่มีประโยชน์ในขั้นตอนนี้คือ แผนผัง SIPOC (ซัพพลายเออร์, อินพุต, กระบวนการ, เอาต์พุต, ลูกค้า) ซึ่งสามารถช่วยคุณ:
- กำหนดขอบเขตของปัญหา
- คิดในแง่ของกระบวนการ
- ระบุให้ชัดเจนว่าอะไรและที่ไหนที่ต้องวัด
- เชื่อมโยงตัวชี้วัดกับปัจจัยนำเข้า กระบวนการ และผลลัพธ์
การใช้ SIPOC คุณกำลังเตรียมเวทีสำหรับการคิดแบบ Y=f(x) ตั้งแต่เริ่มต้น
ขั้นตอนที่ 2. วัด: การระบุตัวแปรสำคัญ
เมื่อคุณได้กำหนด 'Y' ของคุณแล้ว ก็ถึงเวลาที่จะเข้าสู่ขั้นตอน การวัด ในขั้นตอนนี้ จุดมุ่งหมายคือการรวบรวมและวิเคราะห์ข้อมูล ในขั้นตอนนี้ คุณต้อง:
- วางแผนโครงการของคุณเพื่อระบุสาเหตุที่อาจเกิดขึ้นของตัวแปร 'x'
- กำหนดตัวแปร 'x' ที่มีอิทธิพลมากที่สุดต่อ 'Y'
- จัดลำดับความสำคัญและจำกัดจำนวนตัวแปร 'x' ในรายการของคุณให้เหลือเพียงจำนวนที่จัดการได้
- รวบรวมข้อมูลรอบ ๆ 'Y' และ 'x' ปัจจุบันเพื่อสร้างฐานข้อมูลเริ่มต้น
นี่เป็นขั้นตอนที่สำคัญมาก เนื่องจากขาดข้อมูลที่สำคัญอาจนำไปสู่ความล้มเหลวในอนาคตได้ หลีกเลี่ยงการตัดสินใจโดยใช้ความรู้สึกหรือประสบการณ์ส่วนตัว แทนที่จะทำเช่นนั้น ให้เน้นการรวบรวมข้อมูลที่มั่นคงเพื่อช่วยให้การตัดสินใจของคุณดีขึ้น
อ่านเพิ่มเติม:แม่แบบ Six Sigma ฟรี
ขั้นตอนที่ 3. วิเคราะห์: จัดลำดับความสำคัญของสาเหตุที่แท้จริง
เข้าสู่ขั้นตอน วิเคราะห์ เป้าหมายของคุณคือการตรวจสอบและวัดความสัมพันธ์ระหว่าง 'x' และ 'Y' นี่คือจุดที่สูตร Y=f(x) มีบทบาทสำคัญ ใช้เครื่องมือทางสถิติและกราฟิกเพื่อ:
- ทดสอบความสัมพันธ์ระหว่าง 'x' และ 'Y'
- ระบุตัวแปร 'x' ใดที่มีส่วนช่วยมากที่สุดต่อปัญหาในกระบวนการของคุณ
- ตามผลกระทบที่อาจเกิดขึ้นต่อผลลัพธ์ ให้จัดลำดับความสำคัญของสาเหตุที่แท้จริงเพื่อดำเนินการตรวจสอบและปรับปรุงต่อไป
ขั้นตอนนี้เกี่ยวกับการรวบรวมเบาะแสเพื่อการปรับปรุงและระบุปัจจัยสำคัญที่สุดที่ส่งผลต่อผลลัพธ์ของคุณ ในการ ระบุสาเหตุที่แท้จริงของความแปรปรวนของผลลัพธ์ คุณสามารถใช้เครื่องมือต่างๆ เช่นแผนภูมิปลา (Fishbone Diagram), 5 Whys หรือการวิเคราะห์โหมดความล้มเหลวและผลกระทบ (FMEA)
เทมเพลต Process FMEA Lean Six Sigma ของ ClickUpได้รับการออกแบบมาเพื่อช่วยให้คุณระบุความเสี่ยงที่อาจเกิดขึ้นและควบคุมกระบวนการต่างๆ
แม่แบบที่ครอบคลุมนี้ช่วยให้ง่ายต่อการ:
- ระบุความเสี่ยงที่อาจเกิดขึ้นในกระบวนการได้อย่างรวดเร็วและแม่นยำ
- เข้าใจว่าส่วนใดที่ต้องการการปรับปรุง
- สร้างแผนปฏิบัติการเพื่อการปรับปรุง
ขั้นตอนที่ 4. ปรับปรุง: พัฒนาวิธีแก้ไขและทดสอบ
เมื่อคุณมีความเข้าใจอย่างชัดเจนเกี่ยวกับตัวแปร 'Y' และตัวแปร 'x' ที่สำคัญแล้ว คุณพร้อมที่จะก้าวเข้าสู่ขั้นตอน ปรับปรุง
ในขั้นตอนนี้ คุณจะทำ:
- ระดมความคิดสร้างสรรค์เพื่อหาวิธีแก้ปัญหาโดยอิงจากสิ่งที่คุณได้เรียนรู้เกี่ยวกับกระบวนการนี้ วิธีแก้ปัญหาเหล่านี้ควรมุ่งเน้นไปที่การปรับเปลี่ยนปัจจัยนำเข้า (x) เพื่อให้ได้ผลลัพธ์ที่ต้องการ (Y)
- พัฒนาและทดสอบโซลูชันเหล่านี้โดยใช้การทดลองหรือโครงการนำร่องในสภาพแวดล้อมที่ควบคุมได้
- มุ่งเน้นไปที่การแก้ปัญหาที่ตอบสนองตัวแปร 'x' หลักของคุณอย่างแท้จริงและช่วยปรับปรุง 'Y'
- มุ่งเน้นการปรับปรุงที่สามารถตรวจสอบได้ผ่านการวัด
ขั้นตอนที่ 5. การควบคุม: การเพิ่มประสิทธิภาพผลลัพธ์
ขั้นตอนควบคุม เป็นจุดที่ DMAIC แสดงศักยภาพอย่างแท้จริง นี่คือขั้นตอนที่เน้นการรับรองว่าการปรับปรุงของคุณจะคงอยู่และนำไปสู่ความสำเร็จในระยะยาว เพื่อดำเนินการนี้:
- สร้างแผนภูมิการจัดการกระบวนการเพื่อแสดงภาพการไหลของกระบวนการใหม่
- ระบุจุดตรวจสอบที่สำคัญในกระบวนการ
- ติดตามทั้ง 'x' และ 'Y' ตลอดระยะเวลาเพื่อให้แน่ใจว่าการปรับปรุงอย่างต่อเนื่อง
- จัดตั้งมาตรการควบคุมเพื่อรักษาประสิทธิภาพที่ดีขึ้นและป้องกันการถดถอยกลับไปยังขั้นตอนก่อนหน้า
โดยการปฏิบัติตามขั้นตอนเหล่านี้ คุณไม่ได้เพียงแค่ใช้สูตร Y=f(x) เท่านั้น แต่คุณกำลังสร้างระบบสำหรับการปรับปรุงอย่างต่อเนื่องและความสำเร็จในโครงการของคุณ
อ่านเพิ่มเติม:วิธีใช้แผนภูมิควบคุมในการบริหารโครงการ
แนวทางปฏิบัติที่ดีที่สุดสำหรับ Y=f(x) ในการบริหารโครงการ
เพื่อให้ได้ประโยชน์สูงสุดจาก Y=f(x)ในการดำเนินโครงการ คุณต้องปฏิบัติตามแนวทางสำคัญบางประการ แนวทางเหล่านี้จะช่วยให้คุณใช้เครื่องมืออันทรงพลังนี้ได้อย่างมีประสิทธิภาพและบรรลุตัวชี้วัดความสำเร็จในการบริหารโครงการของคุณ
การเลือกตัวชี้วัดที่เหมาะสม
เมื่อดำเนินการ Y=f(x) สิ่งสำคัญคือการเลือกข้อมูลที่เกี่ยวข้องและตัวชี้วัดที่ถูกต้อง เริ่มต้นด้วยการกำหนดเป้าหมายของโครงการให้ชัดเจน ถามตัวเองว่าคุณต้องการข้อมูลเชิงลึกหรือผลลัพธ์เฉพาะอะไร การนี้จะช่วยนำทางการเลือกข้อมูลและเทคนิคการแสดงผลของคุณ
จำไว้ว่า Y=f(x) คือการเข้าใจความสัมพันธ์ระหว่างข้อมูลนำเข้า (x) และผลลัพธ์ (Y) เพื่อทำสิ่งนี้อย่างมีประสิทธิภาพ:
- ใช้ซอฟต์แวร์ประมวลผลทางสถิติเพื่อตรวจสอบว่าการผสมผสานของข้อมูลนำเข้าเฉพาะมีผลกระทบต่อผลลัพธ์อย่างไร
- รวมข้อมูลที่สำคัญให้มากที่สุดเท่าที่จะเป็นไปได้ซึ่งเชื่อมโยงกับผลลัพธ์
โดยการตั้งค่าสูตรอย่างถูกต้อง คุณจะมีความพร้อมมากขึ้นในการเลือกเครื่องมือที่เหมาะสมเพื่อตรวจสอบความสัมพันธ์ระหว่าง X-Y วิธีการนี้ช่วยให้คุณเข้าใจสาเหตุและผลลัพธ์ วัดประสิทธิภาพ และระบุพื้นที่ที่ต้องปรับปรุงในโครงการของคุณ
การใช้ประโยชน์จากการแสดงข้อมูล
การนำเสนอข้อมูลด้วยภาพเป็นพันธมิตรที่ทรงพลังเมื่อทำงานกับ Y=f(x) มันเป็นการผสมผสานระหว่างศิลปะและวิทยาศาสตร์ที่สามารถเพิ่มประสิทธิภาพการบริหารโครงการของคุณได้อย่างมาก นี่คือวิธีที่จะใช้ประโยชน์สูงสุดจากมัน:
- รู้จุดประสงค์ของคุณ: ตัดสินใจว่าคุณกำลังใช้การมองเห็นภาพเพื่อวิเคราะห์หรือนำเสนอ สิ่งนี้จะช่วยกำหนดแนวทางของคุณ
- เข้าใจกลุ่มเป้าหมายของคุณ: ปรับแต่งภาพให้ตรงกับความต้องการ ความสนใจ และระดับความเชี่ยวชาญของทีมคุณ
- เลือกประเภทแผนภูมิที่เหมาะสม: เลือกภาพที่สื่อถึงผู้ชมของคุณได้ดีและช่วยให้พวกเขาสามารถสำรวจข้อมูล, ระบุข้อมูลเชิงลึก, และตัดสินใจได้
การสร้างภาพที่มีประสิทธิภาพช่วยให้ชุดข้อมูลที่ซับซ้อนกลายเป็นเรื่องง่ายขึ้น. ช่วยให้คุณสามารถมองเห็นรูปแบบ, แนวโน้ม, และค่าผิดปกติในข้อมูลที่รวบรวมได้อย่างรวดเร็ว, ซึ่งนำไปสู่การตัดสินใจที่มีข้อมูลรองรับมากขึ้น.
อ่านเพิ่มเติม:ประเภทของแผนภูมิสำหรับการแสดงข้อมูลโครงการ
มุ่งเน้นการปรับปรุงอย่างต่อเนื่อง
Y=f(x) ไม่ใช่แค่เครื่องมือที่ใช้ครั้งเดียวเท่านั้น แต่เป็นกรอบแนวคิดสำหรับการปรับปรุงอย่างต่อเนื่อง นี่คือกลยุทธ์บางประการเพื่อให้มั่นใจว่าจะมีการพัฒนาอย่างต่อเนื่อง:
- ใช้ในทุกขั้นตอนของการแก้ปัญหา: ใช้สมการ Y=f(x) ตั้งแต่เริ่มต้นเพื่อให้แน่ใจว่าคุณกำลังแก้ไขปัญหาที่ถูกต้องด้วยสูตรที่ถูกต้อง
- ปฏิบัติตามแผนที่ DMAIC: แนวทางที่มีโครงสร้างที่เราได้อธิบายไว้ก่อนหน้านี้สอดคล้องอย่างสมบูรณ์กับ Y=f(x)
- สร้างแผนภูมิการจัดการกระบวนการ: สิ่งนี้ช่วยให้มองเห็นภาพการไหลของกระบวนการใหม่หลังจากการปรับปรุง ระบุจุดตรวจสอบที่สำคัญและกำหนดการดำเนินการเมื่อกระบวนการเบี่ยงเบนจากแผน
- รวบรวมและตรวจสอบข้อมูล: ตรวจสอบให้แน่ใจว่าข้อมูลของคุณถูกต้อง สม่ำเสมอ และจัดระเบียบในรูปแบบที่เหมาะสมสำหรับการแสดงผลข้อมูล ซึ่งมีความสำคัญอย่างยิ่งต่อการได้มาซึ่งข้อมูลเชิงลึกที่เชื่อถือได้และมีความหมาย
- ตีความและวิเคราะห์อย่างสม่ำเสมอ: ใช้เวลาในการตีความภาพข้อมูลของคุณและระบุข้อมูลเชิงลึกที่สามารถนำไปปฏิบัติได้ กระบวนการนี้ที่ดำเนินอย่างต่อเนื่องจะช่วยให้โครงการของคุณอยู่บนเส้นทางที่ถูกต้องและตอบสนองต่อการเปลี่ยนแปลงได้
💡เคล็ดลับมืออาชีพ:ผู้จัดการโครงการ AI ใน ClickUpช่วยให้คุณวิเคราะห์ข้อมูลจากหลายแหล่งและระบุความแตกต่างหรือค่าผิดปกติได้ ตั้งค่าการทำงานอัตโนมัติเพื่อแจ้งเตือนทีมของคุณเมื่อกระบวนการใดต้องการความสนใจ
ด้วยการนำแนวทางปฏิบัติที่ดีที่สุดเหล่านี้ไปใช้ คุณจะสามารถใช้ประโยชน์จากพลังทั้งหมดของ Y=f(x) เป็นเครื่องมือสำหรับการปรับปรุงอย่างต่อเนื่อง การตัดสินใจที่ขับเคลื่อนด้วยข้อมูล กลยุทธ์ขององค์กร และความสำเร็จของโครงการ
วิธีจัดการโครงการที่ใช้ Y=f(x) ด้วย ClickUp
การบริหารโครงการอย่างมีประสิทธิภาพต้องการเครื่องมือที่หลากหลายซึ่งสามารถปรับตัวให้เข้ากับลักษณะที่เปลี่ยนแปลงได้ของการบริหารโครงการ ClickUp เป็นเครื่องมือการบริหารโครงการแบบครบวงจรที่นำเสนอแนวทางแบบบูรณาการในการบริหารโครงการที่มีพื้นฐานจาก Y=f(x) ทำให้เป็นเครื่องมือที่ขาดไม่ได้สำหรับผู้จัดการโครงการ
โดยการใช้ประโยชน์จากคุณสมบัติที่หลากหลาย ผู้จัดการโครงการสามารถมั่นใจได้ว่าทุกตัวแปรได้รับการพิจารณาอย่างครบถ้วน ปรับปรุงให้เหมาะสม และสอดคล้องกับผลลัพธ์ที่ต้องการ
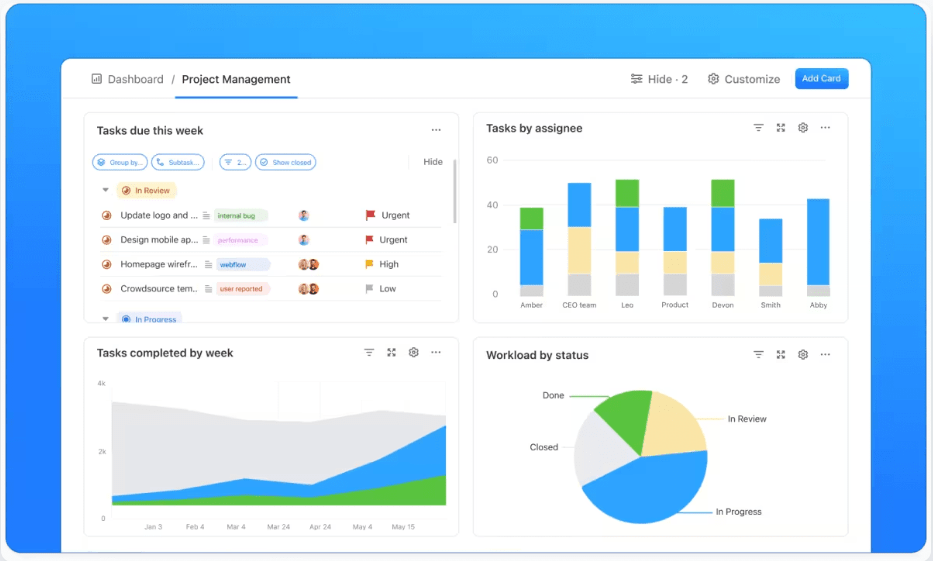
ประโยชน์ของการใช้ ClickUp สำหรับโครงการที่ใช้แบบจำลอง Y=f(x)
แม้ว่าจะมีข้อดีมากมายในการใช้ ClickUp สำหรับการจัดการโครงการที่ใช้ Y=f(x) เป็นฐาน แต่ต่อไปนี้คือประโยชน์หลักบางประการ:
- การควบคุมแบบรวมศูนย์: เก็บตัวแปรและผลลัพธ์ของโครงการทั้งหมดไว้ในที่เดียว ทำให้มองเห็นภาพรวมได้ง่ายขึ้นและตัดสินใจได้อย่างมีข้อมูล
- ความยืดหยุ่น: ปรับเปลี่ยนและปรับแต่งแพลตฟอร์มให้เหมาะสมกับความต้องการเฉพาะของโครงการคุณ ไม่ว่าจะเป็นอุตสาหกรรมหรือขอบเขตใดก็ตาม
- การทำงานร่วมกันแบบเรียลไทม์: ทำงานร่วมกับสมาชิกในทีมในภารกิจและเอกสารต่าง ๆ แบบเรียลไทม์ เพื่อให้มั่นใจว่าจะได้รับข้อเสนอแนะทันทีและแก้ไขปัญหาได้ร่วมกัน
- เพิ่มประสิทธิภาพ: ทำงานได้มากขึ้นในเวลาที่น้อยลงด้วยฟีเจอร์ AI และระบบอัตโนมัติที่ผสานรวมใน ClickUp
นี่คือวิธีที่คุณสามารถใช้ความสามารถของ ClickUp เพื่อดำเนินกลยุทธ์การจัดการโครงการ Y=f(x) ของคุณ:
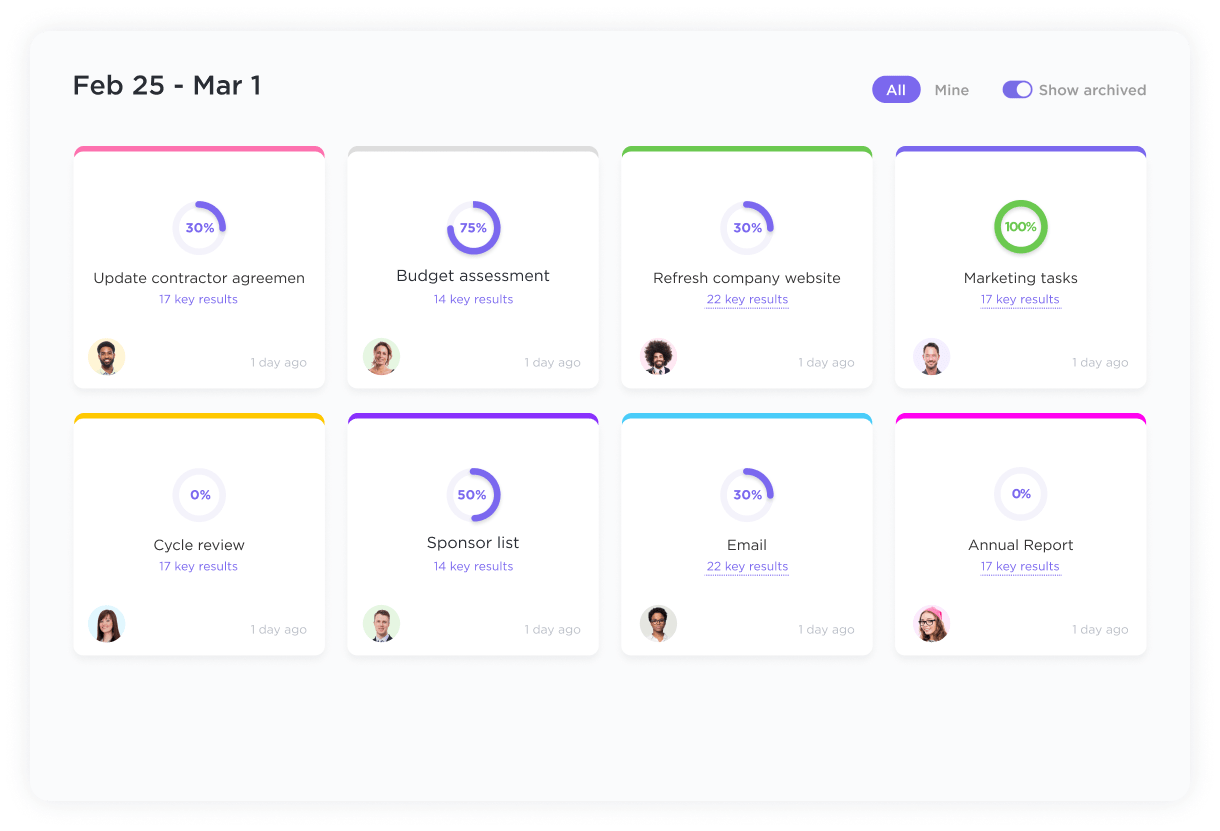
- การตั้งเป้าหมาย: กำหนดผลลัพธ์ที่ชัดเจนและวัดผลได้ (Y) สำหรับโครงการของคุณด้วยClickUp Goalsและติดตามความคืบหน้าในการบรรลุเป้าหมายเหล่านั้น
- การอัตโนมัติของกระบวนการทำงาน: ปรับปรุงกระบวนการทำงานให้มีประสิทธิภาพมากขึ้นโดยการอัตโนมัติงานที่ทำซ้ำและกระบวนการทำงานที่น่าเบื่อโดยใช้ClickUp Automationsเพื่อลดความเสี่ยงจากข้อผิดพลาดของมนุษย์และประหยัดเวลา
- การมองเห็นงาน: มองเห็นข้อมูลโครงการของคุณในหลายมุมมองของ ClickUp ตั้งแต่รายการง่ายๆ ไปจนถึงแผนภูมิแกนต์ที่ซับซ้อน
- ปัญญาประดิษฐ์แบบบูรณาการ: ใช้ClickUp Brainเพื่อคาดการณ์ระยะเวลาของงาน กำหนดเส้นตายที่เป็นจริง และเตือนคุณเมื่อใกล้ถึงกำหนด
- การติดตามความคืบหน้า: รับภาพรวมระดับสูงเกี่ยวกับสถานะและตัวชี้วัดประสิทธิภาพของโครงการของคุณด้วยแดชบอร์ด ClickUpที่สามารถปรับแต่งได้
- เทมเพลต: ใช้เทมเพลตการจัดการโครงการที่สร้างไว้ล่วงหน้าของ ClickUp เพื่อนำวิธีการปรับปรุงที่มีโครงสร้างมาใช้กับโครงการของคุณ
เทมเพลต DMAIC ของ ClickUpช่วยให้คุณจัดการและติดตามโครงการ DMAIC (กำหนด, วัด, วิเคราะห์, ปรับปรุง, ควบคุม) ได้อย่างมีประสิทธิภาพ เทมเพลตไวท์บอร์ดนี้จะช่วยให้คุณนำแนวทางที่เป็นระบบมาใช้เพื่อปรับปรุงกระบวนการและเพิ่มประสิทธิภาพการทำงาน ใช้เพื่อ:
- กำหนดวัตถุประสงค์และกำหนดขอบเขตของโครงการ
- ระบุและติดตามตัวชี้วัดสำคัญ
- วิเคราะห์ข้อมูล, ระบุสาเหตุที่แท้จริง, และนำมาซึ่งการเปลี่ยนแปลง
- รับข้อมูลเชิงลึกด้วยการรายงานอย่างต่อเนื่อง
การจัดการและเพิ่มประสิทธิภาพของ 'x' ใน Y=f(x) ด้วย ClickUp
ด้วย ClickUp คุณสามารถจัดการกระบวนการโครงการของคุณได้อย่างละเอียดและเพิ่มประสิทธิภาพของ 'x'—ปัจจัยและข้อมูลต่างๆ ที่มีผลต่อความสำเร็จของโครงการของคุณ นี่คือวิธีการ:
- การจัดการงาน: แยกตัวแปรของคุณ (x) ออกเป็นขั้นตอนที่สามารถดำเนินการได้ในClickUp Tasks, มอบหมายงานให้กับสมาชิกทีมที่เกี่ยวข้อง และติดตามกิจกรรมของทีมอย่างใกล้ชิด
- ฟิลด์ที่กำหนดเอง: ปรับแต่งงานและจุดข้อมูลของคุณให้ครอบคลุมทุก 'x' ที่เกี่ยวข้อง เพื่อให้แน่ใจว่าการติดตามและการวิเคราะห์เป็นไปอย่างครบถ้วนสมบูรณ์
- การพึ่งพา:กำหนดความสัมพันธ์ระหว่างงานเพื่อให้การเปลี่ยนแปลงในพื้นที่หนึ่งอัปเดตพื้นที่ที่เกี่ยวข้องโดยอัตโนมัติ รักษาความสอดคล้องกับกลยุทธ์ Y=f(x) ของคุณ
- เป้าหมายสำคัญ: เปลี่ยนงานสำคัญให้กลายเป็นเป้าหมายสำคัญของโครงการที่คุณสามารถติดตามได้ เพื่อให้ควบคุมความคืบหน้าของโครงการได้อย่างมีประสิทธิภาพ
อ่านเพิ่มเติม:เทคนิคการประมาณราคาโครงการ
การใช้ ClickUp เป็นเครื่องมือการจัดการโครงการที่มีประสิทธิภาพ
ClickUp ก้าวไปไกลกว่าซอฟต์แวร์การจัดการโครงการแบบดั้งเดิมด้วยการนำเสนอชุดคุณสมบัติที่อำนวยความสะดวกไม่เพียงแค่การจัดการเท่านั้น แต่ยังรวมถึงการทำงานร่วมกันและการสื่อสารอีกด้วย:
- การกำหนดขอบเขต: รวบรวมและจัดทำรายละเอียดความต้องการของโครงการจากผู้มีส่วนได้ส่วนเสียทุกฝ่ายโดยใช้แบบฟอร์ม ClickUp ที่ปรับแต่งได้ และเปลี่ยนข้อมูลที่ส่งเข้ามาให้เป็นงานที่สามารถติดตามได้
- การวางแผน: ตรวจสอบให้แผนโครงการมีความแน่นหนาโดยให้ผู้มีส่วนได้ส่วนเสียและสมาชิกทีมมีส่วนร่วมในการระดมความคิดและสรุปรายละเอียดโครงการด้วยClickUp WhiteboardsและClickUp Mind Maps
- การตัดสินใจ: ตัดสินใจได้ดีขึ้นด้วยแหล่งข้อมูลเดียวที่เป็นความจริงสำหรับข้อมูลทั้งหมดของคุณในClickUp Dashboards ซึ่งคุณสามารถปรับแต่งได้ด้วยวิดเจ็ตเพื่อให้เหมาะกับความต้องการของคุณ
- การทำงานร่วมกัน: เพิ่มประสิทธิภาพการทำงานร่วมกันของทีมด้วยระบบส่งข้อความในตัวผ่านClickUp Chat, การแก้ไขและแบ่งปันเอกสารร่วมกันผ่านClickUp Docs และการแจ้งเตือนแบบเรียลไทม์ เพื่อให้ทุกคนทำงานไปในทิศทางเดียวกัน
- การผสานการทำงาน: ใช้ประโยชน์จากการผสานการทำงานกว่า 1,000 แบบของ ClickUpเพื่อเชื่อมต่อเครื่องมืออื่น ๆ ที่คุณใช้ สร้างระบบที่รวมเป็นหนึ่งเดียวสำหรับกิจกรรมการจัดการโครงการทั้งหมดของคุณ
ClickUp คือที่ที่งาน, เอกสาร, เป้าหมาย และการสื่อสารมาบรรจบกันเพื่อสร้างกระบวนการทำงานที่ราบรื่น. มันเตรียมคุณให้พร้อมที่จะนำทางผ่านความซับซ้อนของการจัดการโครงการด้วยความมั่นใจและความแม่นยำ.
การประยุกต์ใช้จริงของ Y=f(x) ในการบริหารโครงการ
สูตร Y=f(x) ไม่ใช่เพียงแค่แนวคิดทางทฤษฎีเท่านั้น แต่เป็นเครื่องมือที่สามารถนำไปใช้ได้จริงในปฏิบัติการประจำวันของการบริหารโครงการ โดยการผสานสูตรนี้เข้ากับแง่มุมต่าง ๆ ของงานโครงการ ผู้จัดการสามารถเพิ่มประสิทธิภาพในการตัดสินใจ ปรับปรุงการบริหารกลยุทธ์ให้มีประสิทธิภาพมากขึ้น และใช้ข้อมูลเพื่อสร้างแบบจำลองการคาดการณ์ได้
Y=f(x) ในการตัดสินใจและการจัดการเชิงกลยุทธ์
การนำ Y=f(x) ไปใช้ในกระบวนการตัดสินใจ หมายความว่า ทุกการตัดสินใจได้รับการสนับสนุนจากความเข้าใจว่าปัจจัยต่าง ๆ จะส่งผลกระทบต่อความคืบหน้าและผลลัพธ์ของโครงการอย่างไร นี่คือวิธีที่คุณสามารถนำไปใช้ได้:
- การวางแผนเชิงกลยุทธ์: ใช้สมการ Y=f(x) เพื่อกำหนดวัตถุประสงค์ที่ชัดเจน (Y) และระบุตัวแปร (x) ที่จะช่วยในการบรรลุเป้าหมายเหล่านี้ ซึ่งอาจเกี่ยวข้องกับการจัดสรรทรัพยากร การปรับระยะเวลา หรือการเปลี่ยนแปลงขอบเขต
- การประเมินความเสี่ยง: ประมาณผลกระทบที่อาจเกิดขึ้นจากความเสี่ยง (Y) โดยพิจารณาจากความน่าจะเป็น (x) และความรุนแรงของความเสี่ยง แนวทางเชิงรุกนี้ช่วยให้สามารถพัฒนาแผนสำรองและกลยุทธ์การลดความเสี่ยงได้
- การติดตามประสิทธิภาพ: ตรวจสอบโครงการที่กำลังดำเนินอยู่โดยการวัดค่า 'Y' เทียบกับผลลัพธ์ที่คาดหวัง หากค่า 'Y' ไม่เป็นไปตามเป้าหมาย ให้ใช้สูตร Y=f(x) เพื่อวิเคราะห์ว่า 'x' ตัวใดที่ต้องปรับปรุง
- การควบคุมต้นทุน: วิเคราะห์ความสัมพันธ์ระหว่างต้นทุนโครงการ (Y) กับปัจจัยต่างๆ เช่น การใช้ทรัพยากร (x) และการเปลี่ยนแปลงขอบเขต
- การจัดการการเปลี่ยนแปลง: ประเมินผลกระทบที่อาจเกิดขึ้นจากการเปลี่ยนแปลง (Y) โดยพิจารณาจากขอบเขต (x) และความซับซ้อน
โดยการฝัง Y=f(x) เข้าไปในกระบวนการบริหารจัดการเชิงกลยุทธ์ ผู้จัดการโครงการสามารถมั่นใจได้ว่าการตัดสินใจของพวกเขาเป็นไปตามข้อมูลและสอดคล้องกับเป้าหมายของโครงการ
Y=f(x) ในการวิเคราะห์ข้อมูลและการสร้างแบบจำลองเชิงคาดการณ์
การวิเคราะห์ข้อมูลและการสร้างแบบจำลองเชิงคาดการณ์เป็นองค์ประกอบที่สำคัญของการบริหารโครงการสมัยใหม่ Y=f(x) ให้กรอบการทำงานสำหรับกิจกรรมเหล่านี้:
- การวิเคราะห์ข้อมูลทางประวัติศาสตร์: ดูโครงการในอดีตเพื่อเข้าใจว่าตัวแปร 'x' ที่แตกต่างกันมีอิทธิพลต่อ 'Y' อย่างไร มุมมองทางประวัติศาสตร์นี้สามารถช่วยให้การวางแผนและการดำเนินโครงการในอนาคตดีขึ้น
- การบริหารมูลค่าที่ได้ (EVM): คำนวณมูลค่าที่ได้ของโครงการ (EV) ตามร้อยละของงานที่เสร็จสิ้น (x)
- การสร้างแบบจำลองเชิงคาดการณ์: ใช้เครื่องมือทางสถิติในการสร้างแบบจำลองว่า การเปลี่ยนแปลงของ 'x' จะส่งผลต่อ 'Y' อย่างไร ซึ่งสามารถช่วยในการคาดการณ์ผลลัพธ์ของโครงการและตั้งความคาดหวังที่เป็นจริงได้
- การปรับปรุงอย่างต่อเนื่อง: นำ Y=f(x) ไปใช้กับวงจรการทดสอบและการปรับปรุงซ้ำอย่างต่อเนื่อง โดยการวิเคราะห์ผลกระทบของการเปลี่ยนแปลงทีละน้อยต่อ 'x' คุณสามารถปรับปรุงประสิทธิภาพของโครงการได้อย่างต่อเนื่อง
- การควบคุมคุณภาพ: ประเมินคุณภาพของผลิตภัณฑ์หรือบริการ (Y) ตามผลการตรวจสอบ (x)
การใช้ประโยชน์จาก Y=f(x) ในการวิเคราะห์ข้อมูลและการสร้างแบบจำลองเชิงคาดการณ์สามารถเปลี่ยนข้อมูลดิบให้กลายเป็นข้อมูลเชิงลึกที่สามารถนำไปใช้ได้ ทำให้ผู้จัดการโครงการสามารถคาดการณ์และกำหนดทิศทางอนาคตของโครงการได้
นำ Y=f(x) ไปใช้เพื่อความสำเร็จในการบริหารโครงการด้วย ClickUp
Y=f(x) เป็นเครื่องมือที่ทรงพลังซึ่งมีผลกระทบอย่างมากต่อความสำเร็จในการบริหารโครงการ แนวคิดนี้ช่วยให้ผู้จัดการโครงการเข้าใจความสัมพันธ์ระหว่างปัจจัยนำเข้าและผลลัพธ์ได้ดียิ่งขึ้น ซึ่งช่วยให้พวกเขาสามารถวางแผนข้อเสนอโครงการในอนาคตได้ดีขึ้น กำหนดเป้าหมายที่เกี่ยวข้อง และปรับปรุงการวัดผลการดำเนินงาน
กรอบงาน DMAIC มอบแนวทางที่มีโครงสร้างในการนำ Y=f(x) ไปปฏิบัติ โดยนำทางโครงการตั้งแต่การกำหนดเป้าหมายไปจนถึงการควบคุมกระบวนการเพื่อความสำเร็จในระยะยาว
เพื่อให้ได้ประโยชน์สูงสุดจาก Y=f(x) จำเป็นต้องเลือกตัวชี้วัดโครงการที่เหมาะสม ใช้การนำเสนอข้อมูลอย่างมีประสิทธิภาพ และมุ่งเน้นการปรับปรุงอย่างต่อเนื่อง ซอฟต์แวร์การจัดการโครงการแบบบูรณาการ เช่น ClickUp มีฟีเจอร์หลากหลายที่ช่วยให้คุณทำสิ่งเหล่านี้และมากกว่านั้นได้ พึ่งพาซอฟต์แวร์นี้เพื่อบรรลุประสิทธิภาพสูงสุด ขับเคลื่อนนวัตกรรม และสร้างผลลัพธ์ที่ดีขึ้นในโครงการของคุณ